11 月杂题补完计划😎
补完就可以在 11 月获得好成绩了捏😃😃😃
想重刷 EVA 了捏。
这些题他妈怎么想到的我草😭
破防就在一瞬间😭
无力到我了😭
真他妈哭了😭
- [SDOI2019] 热闹的聚会与尴尬的聚会
神秘贪心题不会做捏🤗
观察这两个柿子,可以发现如果 越大, 的范围也越大。不妨让 取到最大。
一开始假设请所有人,那么 。我们想让 变大,只可能每次把度数最小的 删掉,并动态维护与相连的度数。用一个类似于 Dijkstra 的东西就能求出来了。
后面求独立集可以随机化。但是还有一个类似的做法。一样考虑每次把度数最小的点加入独立集,然后维护度数,把与之相连的点打上删除标记。那么根据第一问,这里“与之相连的点”的个数一定 ,那么相当于每次消耗 个点可以有一个点加入独立集。则 。显然满足条件。
- [NOIP2011 提高组] 观光公交
朝花夕拾😂
如果你不抽象问题的话很难思考。思考一下可以设 表示到达第 个站用的时间,那么 ,其中 是第 个站人到的最大时间。那么如果 的时候去减少 才能真正实现减少。那么可以减少的状态为 ,不可以则为 ,那么每次就是选最大的连续 段的 之和,其中 为 中等于 的个数。模拟选 次,。
然后用一些数据结构比如线段树维护这些段。每次一个 肯定是选到不能再选或者 为 。那么维护一下可以做到 。懒得写了。
- 模拟赛 18 T2 分发奖励
大家好我是纯纯的飞舞😅😅😅我不会区间加然后询问全部 的个数是多少。这他妈不是直接维护最小值和最小值个数吗???
然后如果可能影响到点 的只可能是 的祖先,所以直接树上 DFS 一波维护线段树就好了。主席树可以减小常数。
- CF840B Leha and another game about graph
和 lvvd 决斗到的题目,两个人都不会做 *2100😎
总度数奇数且 无 时显然无解。
一个很重要的点在于:如果连成一个环对环上节点的奇偶性是没有影响的。所以把所有的环断掉,就成了一棵树。那么在图的 DFS 树上求解,设 表示 子树中的所有点都满足条件,除了 还需要连 条边( 为 )。然后你发现直接根据这个相应地在树上从下至上连就行。
那么这个只可能在 为 的时候失效,因为根没有父亲来与之连边。所以如果有 为 的,直接把其作为根即可;否则随便选一个。至于随便选可能无解吗?根据反证法,如果根还需要连边,而其他节点都已连好,那么总度数为奇数,矛盾😮
- 模拟赛 19 T3 桥梁
枚举不怎么能优化。考虑能不能缩小每次需要遍历的边的范围。
那么注意到(?),最小生成树中,加入一些边,只可能让原来选的变成不选。所以一开始把所有限制的边都加入,再跑最小生成树,此时被选的不管怎么样都一定会被选。类似地,只保留这些一定被选的边,再跑最小生成树,没有被选的再加入限制边也不可能被重新选择,这些边就是一定不会被选的。所以每次只需要在选一定被选的边的基础上看可能被选的边,这个边数神秘分析一下是 级别的。然后就是 的了。哈哈哈什么神秘题目😋😋😋
学习了一下可撤销并查集(不是可持久化并查集):
struct DSU {
int n = 0, tot = 0, fa[N], sz[N], s[N];
void ins() {
n++, fa[n] = n, sz[n] = 1; //插入节点
}
int F(int x) {
return fa[x] == x ? x : F(fa[x]); //即find查找函数
}
void U(int x, int y) { //合并函数
x = F(x), y = F(y);
if (x == y) return;
if (sz[x] < sz[y]) swap(x, y);
s[++tot] = y, fa[y] = x, sz[x] += sz[y];
}
void D() { //删除栈顶边
if (!tot) return;
int y = s[tot--];
sz[fa[y]] -= sz[y], fa[y] = y;
}
void back(int t = 0) {
while (tot > t) D(); //删除到只剩t条边
}
} d;
才发现原来这个思想直接来源于 [HNOI2010] 城市建设。懒得补完导致的😂
- 模拟赛 19 T2 世界
没做出来的原因在于,强行把过 的折返情况拆成了 和 ,导致不知道怎么合并。哥们!!!这不是直接算前缀然后再算对于每个 的答案吗???我他妈是不是傻逼啊🤣🤣🤣设不算折返的答案为 ,那么实际 的答案就是 ,很好线性维护。
至于优先队列维护高度是好写的。值得注意的是我使用了一个二分规避了 lvvd 的不小常数框开根结果😎
- CF908F New Year and Rainbow Roads
为什么不会傻逼贪心题啊😅
每次肯定是在两个相邻的绿色之间思考。那么如果连了这两个绿色的,对于红色 / 蓝色直接两两两边,边上的就与绿色连。然后这样出现了一个环,还可以减掉一条边,那么肯定是减掉最长边。而我他妈直接把减的这条边认为是最边上的😥然后如果绿色之间不连,对于红色 / 蓝色一样这样两两连边,但是不能去掉边了。两种情况取 注意边界就好了。
所以我他妈又是傻逼了。以后能不能稍微思考一下😅
- CF793F Julia the snail
一开始甚至用一段时间想了一个主席树暴力跳的 做法😅
小看了一下发现可以离线。那么询问和绳子按右端点从小到大排之后,设 表示不大于当前右端点从 能跳到的最大高度。每次更新 的绳子就是把 的 更新为 。然后我聪明地无中生有了一个单调性写出了保龄代码。实际上要用个势能线段树维护。但是我是不会的😎
然而还有一种非常聪明的做法。因为每个询问位置不管怎么移动始终不会小于 ,不妨按 即左端点从大到小排序。这时候把绳子看成 ,题目中的接绳子就变成了一个最长前缀覆盖(端点消去了)。因为右端点越小就越有可能更新到询问的贡献。线段树上维护 表示位置始终不小于当前左端点,从 点爬至少一次绳子能够到的最近点,每次把 与 取 (可以下滑到 爬绳子)。那么每次询问就是找到 之间第一个 的最大值 的位置 。说明 都已经覆盖完了,而到 的时候如果再爬任意一条绳子都会出去,下滑答案肯定不优,那么答案就是 。用一个线段树维护区间 ,区间取 就好了😏
- [CSP-S2019] Emiya 家今天的饭
本来是找信心的没想到我是 nt,这么久才切掉🤪
因为出现大于 的主要食材只可能有一种,那么直接枚举这个主要食材,算不合法的,用全部的减掉就行了。每次 DP 按烹饪方法选保证不重复,前缀和优化是 的,总的就是 的。
博君一笑的是在算不合法时我一开始直接拆成了两部分,只有出现大于 的主要食材的和没有的,然后自然在算烹饪方法时重复了(我怎么这么喜欢乱拆😅😅😅)。其实直接在 DP 里面记录 表示前 个,第 个必选,固定的那个食材选出的数量减掉其它的数量为 。还好意识到之后很快就过了😎
- [APIO2012] 守卫
yly:简单题(指紫题并且鲜有人过)😂
一开始想了一个直接让放置点尽量选右和尽量靠左,取交集。不知道为什么挂掉了。
首先对于这种一堆区间的问题。先看看能不能去掉包含的。显然这里是可以的,只需要保留被包含的。那么按左端点从小到大排序,右端点也从小到大。然后每次尽量选最右的一定是最优的。考虑对于一个区间的右端点,如果我们强制不选之后,答案大于了 ,说明就必须选(实际上是想到了这一点的😥)。那么再重新选一个点,在尽量优的前提下,就是这个点的左边的点。然后我们二分找到这个点不能覆盖的区间,显然是一个前缀 和一个后缀 。考虑算出 表示前 个区间最优需要多少个点, 表示后 个区间最优需要多少个点。 正序尽量选右, 倒序尽量选左。然后如果 大于 这个点就是必要的。有一些 corner case 就略过了。
- 模拟赛 20 T2 三色
大家好,我一开始以为自己爆标了写了一个 的做法。然后发现它不能处理区间重复的情况🤓
具体状态定义和 CSP-S T3 挺像的。主要写一下怎么优化。转移大概是这样的:
for (int i = 0; i <= n; i++) {
for (int j = mx[i][2]; j < mn[i][1]; j++) {
for (int k = mx[i][3]; k < mn[i][2]; k++) {
if (i == n) {
add(ans, f[i][j][k]);
continue;
}
add(f[i + 1][j][k], f[i][j][k]);
add(f[i + 1][i][k], f[i][j][k]);
add(f[i + 1][i][j], f[i][j][k]);
}
}
}
那么我们把 看成一个矩阵,只需要在 变化时维护这个矩阵。操作有:把 处的矩阵复制到 处;把每行的和加到某列上;把每列的和加到某行上。维护矩阵每一列和每一行的和。因为行和列交换 在 不等的情况下只有一个会有值,也可以直接维护 。每次行 / 列保留的都是一个区间,可以维护每行 / 列还没有被删掉的状态,只要每个状态只会被删掉一次就是 的。
具体实现的话,开一个总的 vector 维护所有状态,每行 / 列开 vector 维护这行 / 列的合法状态在总的 vector 中的位置(本来是可以用链表或者 deque 但是因为题解是这样写的,就这么写了😎)。因为每次删除行 / 列还会影响到其对应的列 / 行,直接删除比较难搞,就直接对其在总的 vector 中对应位置上打懒惰删除标记,确保不会重复删除贡献。代码中就是把它的值赋成 了。
Code。
- 模拟赛 20 T3 博弈
性质题。
- CF1740F Conditional Mix
好厉害的题,我不会做是理所当然的🥵但是甚至想到了集合补 。
总之,首先把问题转化为分组。然后就是一个一个分发现很难刻画,尝试直接找刻画合法条件的性质。后面的就看题解吧:Link。
- 模拟赛 21 T2 最长上升子序列
为啥就我这么菜😰😰😰
相当于是在相邻两个数之间建出二叉树,然后最长上升子序列就是一颗树从上到下走(当然需要保证能够接起来),然后依次从左到右走完每颗树(不用考虑接合了,因为下一颗树的所有元素一定都比这颗树大)。也就是说要么把层数增加,要么把颗数增加。感觉这一点好像都没有想到🤔是直接根据总共的一层一层来看的😥
然后对于每一层,肯定选的是连续的。然而有更强的结论:除了选开头或结尾那一个一定会把每层选完。至于证明,发现我又不会了😅
然后设 表示处理完第 棵树第 层的最长上升子序列长度,第 层就是原节点。至于第 棵树第 层有多少个元素呢?手玩可以得到 。那么 trivial 的转移就是枚举上一颗树的层数 ,有 ,前缀优化一下就好了。
然后有两个特殊的地方。首先大多数情况下第 层的开头元素比 层的大。但是如果第 层开头元素为 ,第 层的开头元素就会比 层的小,这时候 还可以由 转移过来。类似地,第 层的结尾元素一定会比比 层的小(如果第 层确实生成了新的元素),那么 还可以由 转移过来。
难死我了😫😫😫
- 模拟赛 21 T3 墙([BalticOI 2024] Wall)
比 T2 好懂😅考试的时候以为是一道原神题,方向一直想错了。
因为所有方案的墙高度好算,只需要算所有方案的水位高度之和(而不是水位差之和)。分拆到每个墙 上考虑,就是 的最大值和 的最大值取 。直接前后缀 dp 可以 。
然而还有一个切入点。我们改成判定,也就是枚举这个墙 处的水位高度 ,计算有多少种方案可能使其为 。答案就是 , 表示有多少种方案可以使水位高度为 。而对于这个可以转化为 ,其中 表示有多少种方案可以使水位高度大于等于 。后面容斥 + 线段树维护,懒得写了🤪
这个 trick 在 intercourse 的时候又用到了:Priority Queue 2。
这个 trick 在 mock contest 的时候双用到了,是 T1。
- CF1580D Subsequence
很水的 *2900 欸😎主要是差点忘了把贡献分拆算一个点 / 一条边被经过了多少次这个常见东西😅
- CF1810G The Maximum Prefix
做 dp 要做出 ptsd 了🤮
这次我们吸取了上面 T3 的教训,设 表示前 个前缀和为 的方案数。每次我们枚举前缀最大值 ,转移只保留前缀和 的部分,可以算出前缀最大值 的方案,然后差分就能得到前缀最大值 $ = k$ 的方案了。然而这样是 的。
但是!我们实际算的是 。然后 显然是不合法的,就等于 。也就是我们可以转化为对 差分。然后 dp 需要避免枚举前缀最大值,不妨一开始固定,设 表示前 个离固定的最大前缀和还差 的期望。那么初始 。转移只保留 的部分就好了。最后直接求和,。
- CF1667E Centroid Probabilities
怎么又是容斥题🙂🙂🙂
题目的条件就是对于 ,他的父亲的编号一定比 小, 是根。一个点 是重心的充要条件是 ,即 且它的直接儿子 都有 。先只满足第一个条件,那么 的儿子只可能在 。假设 ,那么需要选 个儿子,即 ,这 个儿子都可以向前面的连边(包括 ),方案是 ; 点本身有 种连法; 子树外还剩下 个点,一样随便连边 。设 表示点 的答案,则 。拆柿子懒得写了,需要用个组合恒等式。然后再容斥掉任意的后代节点是重心的情况,这样的后代节点 只可能有一个,我们枚举 。那么考虑 如何对 产生贡献,需要 在 的子树内,那么我们一直让 跳父亲,跳到的第一个 的节点就是 的概率为 ,这就是它的贡献。后缀和减掉就好了🤗
- CF1924B Space Harbour
重点是维护区间加一个等差数列,区间求和。调不动了,直接 CTJ 了🤮🤮🤮
- 模拟赛 23 T2 即便看不到未来
T1、T3 怎么都是暴力题😰
首先有一个二分的做法。先二分 ,然后对于走不了的两两连边,看有没有环,如果有环就不行,否则走能走的边肯定能走完。显然可以优化建图,那么就是 的。但是会被卡常。为什么考试的时候没有想到呢🤔
正解属于是人类智慧。感觉很对但是就是不知道怎么想到的。权当感性积累吧(

- [POI2006]ZAB-Frogs
妈逼东西我草拟吗。因为开错数组调成狗把了😅😅😅
主要就是维护很多关键点到 矩阵的每个点的最小欧几里得距离。这个东西考虑设 表示只考虑第 行的关键点到 的最小欧几里得距离。那么真正的 答案就是 (省了开方)。直接上李超就好了。顺便复习了一下李超。注意李超应该是开四倍空间的,除非动态开点,以及如果不是每次全局更新它是两个 的。
- [BalticOI 2016 Day2] 交换
首先整个操作肯定是可以放一个二叉树上。
其实思路是比较像的,除了我使用了一个错误的看左儿子的左右儿子和右儿子的左右儿子的分类讨论😎因为后面的可能也会变化所以是假的。定义 表示如果 在节点 ,最优情况下最终会被放到哪里去。这个对于每个节点 , 只会是它的祖先节点和祖先节点的儿子节点,是 级别的。用 map 直接存状态然后记搜就行了,总的是 。然后该怎么贪怎么贪。
- ARC147E Examination
考虑怎么判无解。把 和 分别排序之后看有没有存在 的情况,有就无解。但是这样做没有什么很好的性质🤔写出一个非常神奇的等价条件:,有 。可以考虑一个一个看 ,每次加完都要满足 。
那么首先 的是肯定需要交换的,用这些维护出 。因为这个是逐一按前缀满足的,找到第一个 的位置 ,只能引入其它的元素 来使其满足条件,那么它会让 都加上 ,看一下柿子就知道必须要有 。对于所有满足条件的未加入的元素 , 没有影响,因为前面的 一定已经满足条件,那么为了加入的尽量少,选 最大的就好了。 是单调的,直接按 维护,每次把 加入大根堆👌
for (int i = 1; i <= lsh.size() - 1; i++) {
while (q.size() && q.top().first <= i) q2.push(q.top().second), q.pop();
cnt[i] += cnt[i - 1];
while (cnt[i] < 0) {
cnt[i]++;
cnt[q2.top()]--;
q2.pop();
ans++;
}
}
- AGC034C Tests
一开始的方向错飞了😥小看一下题解发现可以从 全部为 的时候开始思考,一个一个加其贡献。如果你固定了 那么 的时候 取 ,否则取 (唯一想到的)。那么我写了一个二分加的个数之后跑一个堆维护贪心,始终取贡献最多的,但是不知道为什么 WA 飞了。
然后结果又尼玛是神笔性质题。因为 ,有一个结论:最多只会有一个 。假设有两个 ,不妨 。那么把 加 , 减 ,贡献为 ,是不劣的( 可能有变化,但是 只可能变大, 只可能变小,更不劣)。这样调整一定就能调整到最多一个的情况。然后随便做了😅
- BZOJ3441 乌鸦喝水
前后呼应:神秘贪心题不会做捏🤗
感觉还是比较 666 的贪心。首先显然是能喝就喝。然后设 。那么元素 最多能贡献 次,每次只要当前的答案还 就能喝。那么 越小,限制就越大,过程中,一开始所有的都满足条件,然后最小的那些 不能取了,然后次小的那些 不能取了……那么快速计算的方法就是:对于每个 把它处理到失效。
用线段树维护目前所有合法的位置,开一个变量 维护当前所在位置,要么直接全部走完 也不会使 不合法,直接算之后重置 ;要么在中间某一个位置就会使 不合法,线段树二分找到这个位置 ,令 即可。然后继续推向下一个比它大的 。计算贡献是容易的。
- [POI2006]MAG-Warehouse
它为什么是紫题啊🤔除了考察了切比雪夫距离和曼哈顿距离的转换还有什么🤔循环结构吗🤔
总之就是,把点 变成 后,原来的曼哈顿距离是现在的切比雪夫距离。把点 变成 后,原来的切比雪夫距离是现在的曼哈顿距离。
- 模拟赛 24 T2 子序列们
依稀记得曾经是复习过笛卡尔树的。这就是我们 sb liuzimingc 的学习效果😅
直接删对于连续的同色的就会算重,直接钦定每次只删一段颜色相同的段中最左的。然!后!给每个点赋一个删除时间 !
那么相当于每个点的前一个删除时间比它大的点必须和当前颜色不同。然后直接搬到笛卡尔树上, 表示只考虑区间 的答案,每次枚举最大值 分开成 和 。对应到笛卡尔树上就是使 的子树覆盖区间为 ,那么再往前走 就不是最大值了。所以前一个删除时间比它大的点就是 ,判一下能不能转移,然后组合数直接算两个区间合起来的方案(相当于不打乱两边的相对顺序)。
- 模拟赛 24 T3 钙绿
爱恨就在一瞬间。以为打了 60pts 已经很高了,结果是因为自己没有把贡献拆开算导致必须要多记一下选的个数然后在总的 dp 的时候算组合数直接 起飞🤡正解 so close😥
具体的话,,, 是用 个 凑出和为 的方案数,然后每次算一轮 dp 的时候预处理一下 表示在当前空位个数下,放一堆 凑出和为 的方案数。枚举一下非零空位的个数 ,有 $w_j = \sum\limits_{i = 1} ^ j {siz \choose i} f_{i, j} $。这样总的 dp 就是 的。妈的。
- 模拟赛 25 T1 ti
我们惊奇地发现这里出现了一道 T1😅😅😅
重点是对于操作 3 的分析。个人是把它化归成了和操作 2 类似的东西,然后一通搞搞搞搞不出来。实际重点是,操作 3 是每次把开头的放到最后,你会发现这个相当于就是一个环,只是在改变环的起点,就从单纯序列上的神秘移动转化成了环。然后操作 2 的话就是把从任意一个元素到第 个元素拿到开头,对应到环上就是把最后一个拿到任意一个位置。又因为操作 3 可以改变环的起点,那么相当于可以用一次操作 2 和若干次操作 3 把任意一个元素移动到任意一个位置。那么在环上找一个 LIS 就是最多不用改变的,其它的都要变。
- 模拟赛 25 T2 tii
妈的智障。我已经转化成前缀和的形式了😅,也就是最小化 。不知道是不是因为后面这一步没想到所以看不出来化成点😅然后令 ,那么就是最小化 。直接把 视作点 ,就相当于最小化任意不同两点斜率的绝对值。然后注意到只可能是 坐标相邻的两点来贡献,证明考虑反证法,画图显然。类似的,如果是最大化任意不同两点斜率的绝对值,可以考虑交换 后思考,结论:只可能是 坐标相邻的两点来贡献。
总之我就是若只🤗
- 模拟赛 25 T3 tiii
其实思路是差不多的,都是分成正负两边然后用一个类似区间 dp 一样的东西计算(可以化归到类似于关路灯一样的问题)。重点是关于如何限定状态,我是按 来限定的,因为一开始以为每次贡献只是和这个有关,后面发现不对了就直接脑袋宕机了😶然而实际是直接按照 即速度来限定。就是看正 / 负一边“当前还没有追到的鸡的速度的最大值”,设这个鸡的编号为 ,然后我们 dp 还知道了当前时间。如果 说明已经追到了;如果 且当前时间下 到原点的距离不大于 到原点的距离,追到 就一定会追到 ,直接忽略掉;否则如果大于就说明一定还没有追到,是记录在状态里的,后面 dp 会一一追到。这样所有的状态都可以确定了。
- [POI2007] ODW-Weights
甚至不知道题目给的互相是倍数有什么用。只除掉一个 之后就不知道干嘛了😅
然而其实是在告诉你不同数的种类是 级别的。类似的还有比如一堆数的和为 ,那么不同数的种类只是 级别的。然后就变成一个类似于进制一样的东西,从低位到高位依次放,用 DFS 处理借位。
- [POI2007] EGZ-Driving Exam
妈妈生的😶
转化之后和上场模拟赛 T1 很像。都是找到 LIS / LDS 然后减掉。结果我使用了一个贪心去线性求 LDS😅写下来纯是记录自己的脑瘫时刻😅算了至少转化想到了,值得鼓励。
- [POI2007] POW-The Flood
怎么 RETARD 题都不会做了🤔
甚至在题意转换上失败了。这种和水相关的就一直不怎么会。如果在点 放了一个抽水机,能抽到点 当且仅当存在一条从 开始的路径满足 。然后显然的按 从小到大排序 + 并查集。然后在维护的时候,甚至想的是“把在城中的点加入后的集合拿出来然后找覆盖的最小点数”。哥们你直接维护一个集合内部有没有抽水机不就好了。加入的时候如果内部没有抽水机就放一个,因为以后放高度会更高,显然不优。
- [POI2010]KLO-Blocks
艾宾浩斯遗忘曲线(无端
一直在想怎么去调整 的 使得答案最大,然后就死了😅又是尝试刻画性质:最长的一段合法区间需要满足平均数 。如果端点是由外面的贡献而来呢?那么外面的也需要包含进去,然而这样的区间也会被计算。所以这样一定能找到最长的合法区间。
然后就开始套路堆叠了。设 ,如果 合法,则 。可以线性对数做,但是要做到线性。考虑 且 , 一定不会是最优的左端点,可以替换成 ; 一定不会是最优的右端点,可以替换成 。所以可能成为左端点的只能是前缀最小值,可能成为右端点的只能是后缀最大值。搞出来之后用个指针就是线性的了。这实际是模拟赛 12 T2 的 trick,为什么又忘了😣
- ARC125F Tree Degree Subset Sum
其实就是 。那么不同数的种类只是 级别的。考虑证一个神秘性质:令所有 后对于一个固定的 ,合法的 中 一定是连续的(也就是可以直接用最大值减去最小值加一算个数)。此时 ,设 为 的个数。假设对于一个 ,满足的 。只需要证 。因为你可以通过调整选 来从极端值转换,尽量多覆盖。如果 为一合法的数对,则 ,那么把选的点集取反, 也为合法数对。则 ,可以得到 。也就是 。
证明之后只需要算出对于每个 的 最小值和最大值,用单调队列优化背包是 的。也可以二进制拆分。
- ARC106E Medals
重点说一下高维前缀和的部分。相当于枚举选出的人的二进制集合 ,如果 的话 这天就有贡献。总天数是知道的,容斥转化为算 ,即 ,这就可以高维前缀和了。注意高维前缀和枚举某一位是放在外面的。
for (int i = 0; i < n; i++)
for (int j = 0; j < 1 << n; j++)
if (j >> i & 1) f[j] += f[j ^ (1 << i)];
- [POI2011] SEJ-Strongbox
有趣的捏🤩下面的分析避免了加法群啥的。
如果只选一个 ,那么相当于所有 都会加入。相当于所有不大于 的 都会被加入。反证,如果有 不等于 ,即 无解。充要条件为 ,显然不可能,矛盾。
那么对于所有的选择 / 密码都可以化成 的形式。然后显然选任意一个 都可以得到所有不大于 的 。那么化完之后,已经令 ,考虑有没有可能选两个 ,,且 。考虑表示,为了 的存在有必要,应该保证不存在 ,即不存在 。充要条件为 ,显然不可能,矛盾。
所以只可能由一个 扩展而来。然后随便做了。
- 模拟赛 26 T1 定向越野
我:对啊我知道啊?
lxd:然后你就直接 dp 啊。
我:无语凝噎.jpg
妈的。我真他妈是他妈的😊
旋转一定角度之后就是曼哈顿距离。考虑这个角度,一定是跟某两个点有关,即旋转这个角度之后使得某两个点是水平 / 垂直的。枚举 ,设 为旋转角,两点之间欧几里得距离为 ,那么 。这里 取负是因为不取负是两点之间角度相关,你需要反着转抵消这个角度。
然后甚至场推了一个旋转公式, 旋转 之后为 。然后!因为是曼哈顿距离所以就是一堆加减,分母始终是 !然后就只需要算分子了!把上面的式子代进去列一个曼哈顿距离的形式就清楚了。平方是在最后开的。注意比较时乘法开 int128。
- 模拟赛 26 T2 字符串
梅开二度了属于是。
直接跳 KMP 的 数组最坏是 的。考虑如何优化:对于 的 border,这些 border 需要接上新的 ,可能会不再是 的 border;而对于 中不是 border 的前缀,还是不可能满足是 的 border。于是只需要维护上一个位置()合法的 之和,计算只需要每次减掉那些加入 后使得不合法的。然后对于前缀右端点在 及之前的部分,不合法的端点就是在 处不合法的端点(画图看就知道了),于是可以直接继承。剩下的话直接暴力找 的 border,从 不断跳 ,跳到 前就可以直接 break。总的时间复杂度是 。
- 模拟赛 26 T1 数的拆分
原题是黄题。而且我连原题都过不了😐😐😐不嘻嘻😑
一个很重要的点在于:一个大于 的整数一定可以被拆分成若干个 和 之和(小凯的疑惑🤔)。 的情况是 trivial 的,判一下平方 / 立方。然后我们就只需要算 的情况了。那么最小的质因子 一定有 ,也就是只需要筛出大概 以内的质数。然后依次除一定能消掉一项平方 / 立方,最后看剩下来的是不是平方 / 立方就好了。当然中途如果有一个数只能被除一次()就无解。。
- 模拟赛 26 T2 括号序列
爆搜秒了😘
重点是: 位置能否放左括号,只取决于 和 的度数。相当于,把 和 连边,需要选 条边,使得每个点都被选到,同时满足括号序列的限制。然后这样会出现若干个环。显然奇环会导致无解,只可能有偶环。考虑环上一个点如果填了左括号,相邻的只能填右括号,以此类推。那么总共只有 种方案。直接搜索最坏是 ,注意到长度为 的环,一定是编号小的填左括号更优,这样更可能满足前缀和 的限制(经典转化略过了)。那么只需要搜索长度不小于 的环,就是 了。常数很小。
这个连边思想要注意了,Sum Balance 即用到。那里是每个点只会连出一条边,是个内向基环树,一样找环处理。
- [POI2012] ODL-Distance
喜报之我不会 。mdzz。注意到这个(或者不需要注意),设 表示 的质因子次幂和,那么 。显然枚举 然后随便做了。不知道为什么暴力连边跑 BFS 挂掉了😭放在连出来的树上思考其实就是两点的距离, 就是 在树上的 LCA。
- 模拟赛 26 T4 构造数据
有一个费用提前计算的思想。设 ,那么操作只会进行 次,每次选两个不同的数。不妨拆开成单个数思考,统一对于一个 全部放完。就相当于有 个盒子,每个盒子只能装两个不同的数。那么,每次对于一个 ,只需要保证一个盒子最多放一个。后面的 dp 就挺 OK 了:😎
emoji 放链接,酷到我了。
- AGC018C Coins
一个很神奇的东西:按 从小到大排序,那么一定选金的全部都在选银的后面,否则交换一定不劣。考虑默认选铜,化成 ,这样选出来的就是抵消了铜的贡献的。然后就转换成前 / 后 个数的 的前 大之和。厉害哦哦哦😯
- [POI2012] SQU-Squarks
因为完全做不动今天的贪心题😣跑来做这个了。一下子变得小清新了😙Confidence attained.
假设原数组 从小到大排序。那么和数组是这样的:
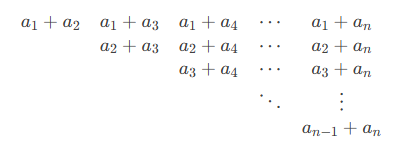
那么如果知道 ,就能知道 ,因为 一定是最小的,删去 后,能知道 ,因为 一定是最小的。删去 、 后,能知道 ,因为 一定是最小的……如果知道了 ,就可以在 的时间复杂度内得到原数组。如果直接枚举是 的。
考虑 、 一定是最小和次小的,这是已知的。如果知道了 就能算出 ,而 一定是在和数组的前 个中,枚举 ,然后计算,就是 。
- [POI2012] WYR-Leveling Ground
神仙题。所以我不会做是理所应当的😏
考虑差分数组,记为 ,相当于就是在任意 ()加减 或者 ,只需要满足加 / 减 的个数相同,及加 / 减 的个数相同,就能两两配对。这样我们只关心差分数组的加减了。对于一个 ,直接上 exgcd 解出一组特解满足 。然后因为后面需要调整,可以求出 ,这样可以改为 。
先不考虑数量相同的限制。那么总的答案就是 。这个显然只会在 或者 取到小于等于 的最大值或大于等于 的最小值时最小。很好讨论。那么得到这个之后,我们希望通过调整使得加 / 减 的个数相同,及加 / 减 的个数相同。前者满足后者自然成立。只需要看前者。等价于 。那么当 时,我们需要进行 次操作,每次操作一个 让它增加 , 减少 。那么这样会带来新的贡献,。这 次操作是必须完成的,我们只需要每次都选择贡献变化量最小的操作,实际就是一个反悔贪心的过程。 类似。
- [POI2012] LIC-Bidding
dp 注意实际状态数,在呀!土豆!博客里有相关的。这里 ,只需要用 表示,状态数是 。这样时间复杂度就对了。我是 nt 又没看出来🤣🤣🤣
甚至还是 的状态,出现在了 11.25 的晚测中🤔链接:「KDOI-11」飞船。
- 模拟赛 28 T3 排序
不知道性质怎么办捏😥**一个数后面所有小于它的数会随着这个数一起运动。那么我们把它们打包成一段,以起始元素来代表一整段。每次操作就是找到跨过 到 的一段,把它从 到 中间断开,然后重新分段后按每段的起始元素从小到大排序。**设 表示下一个比 大的元素,把 重新分段就是分成 ,以此类推。
每次如果有分裂操作一定会多出至少一段,只需要 次就一定能操作完毕。因此可以 。按权值记录以这个元素为起始元素的段的长度,可以用 BIT / 权值线段树等维护,二分前缀和就能够找到某一个起始元素的位置,就相当于自动排序了,通过记录权值对应的下标和二分出来的剩余距离可以算出任意元素的实际位置。然后只需要通过单点加去修改作为起始元素的长度,即,从 开始不断跳 。总的时间复杂度是 。
- [POI2011] DYN-Dynamite
因为懒所以没有写总结,发现另一道题出现相同套路差点忘了,属予作文以记之🙄🙄🙄感觉是蛮经典的。
二分 ,那么关键结点必须满足到至少一个选出来的点的距离 ,这样的关键结点就是“已覆盖的”。直接给出做法:设 为 子树内最远的未被覆盖的关键点到 的距离, 为 子树内最近的选出来的点到 的距离。就很在 LCA 处贪心的感觉。初值和转移是 naive 的。
for (int i = 1; i <= n; i++) f[i] = -inf, g[i] = inf;
void dfs(int u, int fa, int mid) {
if (key[u]) f[u] = 0;
for (int v : e[u]) {
if (v == fa) continue;
dfs(v, u, mid);
if (f[v] != -inf) f[u] = max(f[u], f[v] + 1);
if (g[v] != inf) g[u] = min(g[u], g[v] + 1);
// ...
}
考虑如何处理变化。首先如果 ,没有关键点,直接跳过。否则如果 ,不需要新的点,光是子树内的点自然就覆盖完了,令 ;否则说明覆盖不完了,我们一定会在 或 的祖先上选择一个点。那么,如果 ,其中 是 到父亲的边权(根节点则 ),我们不能再往父亲推了,必须在 放,令 。
上面说的题目:[COCI2021-2022#4] Parkovi。
- CF865D Masha and Cactus
首先处理加的边肯定是在 LCA 处。设 表示 子树的答案,如果 处没有任何可以加的,。如果选择了一个可以加的,假设为 ,那么 到 到 上的点都不能贡献了,只可能是它们没有在 到 到 上的子节点来贡献。然后有一个很厉害的容斥:维护 ,这样只需要把 到 到 上的 全部加起来再加上 就是它们“没有在 到 到 上的子节点”的贡献。然后可以树剖维护。类似的容斥方法还比如记点 的权值为 ,其中 为 的子节点个数。这样一个子树的权值和始终为 (之前模拟赛的 dp 题)😎
- AGC020F Arcs on a Circle
无感而发:语言学教育任重道远😃
简单处理略过。重点在于把线段的起始位置拆成整数和小数部分,因为长度也是整数,只需要单独比较整数部分与整数部分 / 小数部分与小数部分就好了。那么可以 枚举小数部分的大小关系。这样的话,有用的点(即端点)只有 个。就可以每次暴力 dp 了。这里 dp 状态也值得注意:设 表示处理完左端点 的,右端点最大为 ,选择线段的集合为 的方案数。通过记录右端点来看如何覆盖的,更深入的一道题:Gerald and Path。
- ARC118E Avoid Permutations
Link 写的挺好。这类除了那种冷幽默不会的 dp 还可以直接按容斥系数 dp,直接记录在状态中。至于这里怎么保证排列不重?还是看成点 。因为行数、列数只会增加,dp 直接记录当前行和当前列是不是已经被 ban 掉了,如果都没有当前点就可以选择。
发现现在不喜欢用 emoji 了😕😕😕所以多用一点🤗🤗🤗🤗🤗
- [NOI Online #1 提高组] 冒泡排序
一轮冒泡排序本质:从第一个数开始,插入到第一个比它大的数的左边,以这个比它大的数重新开始。设 表示 前面比 大的数个数,一轮冒泡排序就使得所有的 。这样一般会维护 来做🥰🥰🥰
- [POI2015」Podział naszyjnika
很 edu 的题目😍肯定有一段是在区间内的。所以环其实没必要特殊处理。线段树做法略过了。主要是特定区间上的线段树二分:
int ask_l(int p, int l, int r) { // [l, r] 内最左的为 1 的点
if (l <= t[p].l && t[p].r <= r) {
if (!t[p].sum) return -1;
if (t[p].l == t[p].r) return t[p].l;
int ans = ask_l(lc, l, r);
if (~ans) return ans;
return ask_l(rc, l, r);
}
push_down(p);
if (l <= mid) {
int ans = ask_l(lc, l, r);
if (~ans) return ans;
}
if (r > mid) return ask_l(rc, l, r);
return -1;
}
还有一个线性做法,但是不知道为什么跑得比线段树还慢。使用高级的哈希维护本质相同区间😎对于一个颜色随机赋权,对于每种颜色的最后一个赋为前面的同种颜色的权值的异或和。这样一个合法区间(要么出现某种颜色的全部,要么根本不出现某种颜色)就是每个位置的权值异或和为 。然后前缀和一下,你就可以 unordered_map + two-pointer 了。
- [清华集训2016] Alice 和 Bob 又在玩游戏
又是 personally educational 的题。为什么是 personally 因为别人都秒掉了😂😂😂
感觉 SG 函数是这样的。计算就是当前状态可以到达的所有状态的 SG 函数的 mex。SG 函数非零则先手胜。所以当前状态是必胜态就直接令 SG 函数为 等非零值就好了,必败态就是 (只要 SG 满足这样的关系就是对的,一些题里面固定的 SG 函数是找规律发现比较好刻画的性质)。然后如果是组合游戏判断就是各个状态 SG 函数的异或和,比如多 Nim 游戏。
以及 01Trie 相关的维护,和权值线段树很像。就是按 Trie 依次模拟走,相当于线段树上维护走到的 的 。然后因为这里算 mex,关注存在性,加入只需要赋为 就好了。这样就可以直接统计不同的个数。
- [JXOI2018] 守卫
是需要 Ni 的题目。因为我不是 INFJ 不惯用 Ni-Fe 轴不是 INFp 不是 IEI 不是 TE 不是白色圆圈和黑色缺一角的正方形所以我不会做是很正常的😡
考虑区间 ,首先 处肯定要放一个。妈的后面懒得写了什么若只题目,看 Link。
- [POI2015] WYC
怎么矩阵快速幂 & 图论相关的退化成狗把了啊😅😅😅
处理边权直接拆点。把点 拆成 ,然后 ,,题目给的边就是 。这样跑 次快速幂就是路径长度刚好为 的,可以通过连 ,相当于不走了, 继承上一次的。很聪明。然后可以倍增这个矩阵,如果能一直走,走 步至少不同路径数为 ,那么只要倍增六十多次看答案有没有到 就好了。最后统计答案一样倍增跳,类 LCA。
int d = 1;
for (; ; d++) {
a[d] = a[d - 1] * a[d - 1];
t = b * a[d];
if (t.a[0][0] - n >= k) break;
if (d > 64) return cout << -1 << endl, 0;
} // 会把长度为 0 也算进去,所以要减 n
for (int i = d; ~i; i--) {
t = b * a[i];
if (t.a[0][0] - n < k) b = t, ans += 1ll << i;
}
- [POI2016] Nim z utrudnieniem
暴力 dp 不说了。关键是优化。这里考虑的是异或的一个性质,一堆 的数异或和一定也 。然后可以按 从小到大排序后,动态维护这个 ,那么大概就是 即 级别的。总的复杂度 。所以为什么不能使用“不同的数种类 ”呢。哦只用这个是 的。
- [ROI 2024 Day 2] 交互式通道
又是被蓝题薄纱的一晚🥱自己做的时候感觉先后如何放很难确定。结果他妈直接拓扑排序确定,我谔谔。
如果两端颜色相同但是路的颜色不同显然无解。然后因为黑色是需要变化才能得到的,所以让尽量多的点都为黑色。考虑 两端分别为黑 / 白,路为黑,那么肯定是 开完黑(?)之后 变白,可以无脑把 开黑放开头,只需要使 变黑在 前面; 两端分别为黑 / 白,路为白,则(如果) 开黑后, 一定会在 变黑之前变白。这样就出来形如“操作 变为它应该变成的颜色要在 变为它应该变成的颜色之前”了。拓扑排序 + 判环秒了。注意如果一个点应该是白色就可以最先让其变成黑色,放最前面是不影响的,然而如果应该是黑色就需要确定什么时候变,不能直接放最前面。
- [NOI2012] 骑行川藏
主要是学习了一下模拟退火。很早以前曾经写过一篇博客但是忘完了😢这里是用的随机两个点,把一个点的 值分出一部分放到另一个点的 值中。注意模拟退火的随机调整部分需要和当前温度 有关。
- ARC092F Two Faced Edges
虽然感觉并没有可扩展性但还是写一下。对于一条边 反向后整张图的强连通分量个数有变化当且仅当恰好满足下列两个条件中的一个:
- 忽略这条边后, 能到达 ;
- 忽略这条边后, 能到达 ;
后面的处理:Link。
- 模拟赛 35 T2 图上问题
发现最近写得越来越简略了。毕竟还有几天了,忍不住想摆😬
自己连树的情况都不会做😂以 为根节点 DFS,因为操作一个点之后,它的所有祖先就不能再选了。放到一个点上去考虑,也就是计算一个点会被操作的概率,由期望的线性性可以直接加起来,轮数是不重要的。那么如果这个点的子树内已经被操作过,就不能再操作这个点了,这个点 的贡献就只会是在 的子树中选择到这一个点,为 。后面边双缩点,扩展一下结论是容易的。
- [GDKOI2024 提高组] 不休陀螺
说实话这个结论是不那么容易的🤨一个区间 合法当且仅当 且 。先贪心把 的放前面,然后如果是在一个 的位置不合法了,就是 ;否则如果要把前面的部分 的放后面去,就是 ,即 。所以每个的贡献就是 ,总的取最大就好了。后面的结论因为 始终成立()所以是有单调性的,所以是可二分的。
- CF2025F Choose Your Queries
和之前决斗的 *2100 题目很像🤔然而我还是没有做出来🤔然而它是 *2700 的🤔
首先放到图上考虑,就是给所有边定向,使得入度为奇数的点的数量尽量少。一样地考虑 DFS 树,DFS 时遵循优先满足儿子的入度为偶数,这么依次往上推,最后推到根节点。如果是树边,根据儿子的当前入度操作;如果是非树边(返祖边),我们不能去动儿子,只能去动父亲,这样才可能依次调整到最优,那么也就是定向到边上深度更小的那个点。注意判一下建树时的双向边。
相思相思相思😇😇😇
- [TJOI2015] 组合数学
看了 Dilworth 定理之后做的。这里直接把 拆成 上有 个点。那么如果 , 是可到达 的。每次都走的是“可到达”关系,要走若干次走完,相当于最小链覆盖。转化为最长反链,即两两都是“不可到达”的。那么 可以直接当作整体加入。其实就相当于是从左往右推 列,如果选一个元素,其行数必须要小于上一个选的行数。随便 dp 一下就好了。不知道为什么题解都写的云里雾里的😖
- 模拟赛 36 T2 山路
省流:对于每个 的 ,求包含点 的最小环。
一开始我说这不 Floyd 秒了,然后发现我只会算特定点是环中编号最大的情况(就是一边更新 Floyd 一边更新答案)😅
所以题解使用了一个分治,类似 CF1442D Sum。记 表示只用编号 的点, 到 的最短路。每次取中点 ,先用 更新最短路,递归 ,回退;再用 更新最短路,递归 回退。最后到叶子节点 时就可以统计了。一次过程是 的,还要枚举两点,总的是 。
还有使用最短路树的做法。最短路树就是只保留可能在最短路上的边拉出来的东西。
对于一个对点 的询问,我们以 为起点跑一次最短路,然后把最短路树建出来,顺便处理出每个点是在 的哪棵子树内。那么一定能找出一条非树边,满足这条非树边的两个端点在根的不同子树中,使得这条非树边 + 两个端点到根的路径就是最小环。
具体看:Link。
- CF1743F Intersection and Union
显然可以设 表示前 个完 的个数。然后不知道怎么优化。然而注意到 始终是定值,等于 ,可以直接设成 表示前 个为 的概率。为 的概率就是 。然后可以化柿子转到线段树上了。
妈的调一个区间赋值区间乘调成寄吧了😋整体 push_down 的时候,先处理赋值,这时候不需要把乘法的标记给去了。。。单独在 push_down_fix 的时候才会去。。。
void push_down_fix(int p, int v) {
t[p].sum = (t[p].r - t[p].l + 1) * v % mod;
t[p].fix = v;
t[p].mul = 1;
}
void push_down_mul(int p, int v) {
(t[p].sum *= v) %= mod;
(t[p].mul *= v) %= mod;
}
void push_down(int p) {
if (t[p].fix) {
push_down_fix(lc, t[p].fix);
push_down_fix(rc, t[p].fix);
t[p].fix = 0;
// t[p].mul = 1;
}
if (t[p].mul != 1) {
assert(!t[p].fix);
push_down_mul(lc, t[p].mul);
push_down_mul(rc, t[p].mul);
t[p].mul = 1;
}
}