Holes To Fill

单调队列

不知道为什么会写这个东西。感觉从来没有搞懂过？？？太菜了👎

类型比较像滑动窗口。大概就是维护“可能成为候选答案的东西”。比如维护 $a$ 的区间最大值，从左往右滑，如果有 $a_i \leq a_j$ 且 $i < j$ ，那么 $i$ 一定不可能成为答案，因为 $a_j$ 的值不仅不劣，还更靠后，对于后面的计算有更多可能。所以维护 $a_i > a_j （i < j)$ ，也就是一个单减序列。

流程一般就是对于每次新加一个元素，先弹掉不合法的队首，然后弹队尾使得加之后还是满足单调性，然后加入元素，更新答案。如上面的例子维护出来是一个单减序列，答案就是队首。

重点的一个部分，虽然很 shabby，就是维护单调队列可以仅维护你要转移的。比如 $f_{i, j}$ ，然后重点在 $j$ 的变换上，你可以只维护转移过来的 $f_{i - 1, k}$ 。就是每次 $i$ 变化可以重新构建单调队列。然后再开始一边维护一边计算答案。注意可能没有合法的情况，不能随便转移，加上 if (head <= tail) 就行。

Take 六出祁山 as an example。

namespace liuzimingc {
const int N = 305, M = 9e4 + 5, INF = 1e9;
#define endl '\n'
#define int long long

int n, d, h[N], v, a[N], ans, q[M];
int f[N][M];
vector<int> lsh;

int get(int x) {
	return lower_bound(lsh.begin(), lsh.end(), x) - lsh.begin();
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	cin >> n >> d;
	for (int i = 1; i <= n; i++) cin >> h[i], v = max(v, h[i]);
	if (abs(h[1] - h[n]) > (n - 1) * d) return cout << -1 << endl, 0;
	for (int i = 1; i <= n; i++)
		for (int j = -n; j <= n; j++) {
			int x = h[i] + j * d;
			if (x >= 0 && x <= v) lsh.push_back(x);
		}
	sort(lsh.begin(), lsh.end());
	lsh.resize(unique(lsh.begin(), lsh.end()) - lsh.begin());
	memset(f, 0x3f, sizeof(f));
	f[1][get(h[1])] = 0;
	for (int i = 2; i <= n; i++) {
		int head = 1, tail = 0, r = 0;
		for (int j = 0; j < lsh.size(); j++) {
			while (head <= tail && lsh[j] - lsh[q[head]] > d) head++; // 维护队头
			while (r < lsh.size() && lsh[r] - lsh[j] <= d) { // 滑动要加的新元素，单调的
				while (head <= tail && f[i - 1][q[tail]] >= f[i - 1][r]) tail--; // 维护队尾
				q[++tail] = r++; // 加入
			}
			f[i][j] = f[i - 1][q[head]] + abs(lsh[j] - h[i]); // 计算答案
		}
	}
	cout << f[n][get(h[n])] << endl;
	return 0;
}
#undef int
} // namespace liuzimingc

Exgcd

souvenir

可以用来求解同余方程 $ax + by = \gcd(a, b)$ 。当然你可以把结果框在一些范围内啥的。

faire

递归式，求解 gcd 的时候顺便求了。设递归下去的 $a' = b, b' = a \bmod b$ ，已经求出一组解 $a'x_0 + b'y_0 = \gcd(a', b')$ ，则 $a'x_0 + b'y_0 = \gcd(a, b)$ 。代入有 $bx_0 + (a \bmod b)y_0 = bx_0 + (a - \lfloor \dfrac{a}{b} \rfloor b)y_0 = \gcd(a, b)$ 。打开括号，交换一下有 $ay_0 + b(x_ 0 - \lfloor \dfrac{a}{b} \rfloor y_0)$ 。然后就有解 $x = y_0, y = x_0 - \lfloor \dfrac{a}{b} \rfloor y_0$ 。边界 $b = 0$ 时，有特解 $x = 1, y = 0$ 。

int exgcd(int a, int b, int &x, int &y) {
	if (!b) {
		x = 1, y = 0;
		return a;
	}
	int g = exgcd(b, a % b, x, y);
	int t = x;
	x = y;
	y = t - (a / b) * y;
	return g;
}

quelque chose

对于 $ax + by = c$ ，先解 $ax + by = \gcd(a, b)$ ，得到 $ax_0 + by_0 = c$ 。如果 $\gcd(a, b) \nmid c$ 则无解。然后需要改变答案， $x_0, y_0$ 乘上 $\dfrac{c}{\gcd(a, b)}$ 即可。然后框定范围，因为改变 $x_0, y_0$ 后结果不变，那么设 $x_0$ 增加量为 $k_1$ ， $y_0$ 减少量为 $k_2$ ，则 $ak_1 = bk_2$ 。发现只要 $k_1 = \dfrac{b}{\gcd(a, b)}k, k_2 =\dfrac{a}{\gcd(a, b)}k$ 即可。

也就是说， $x = x_0 + \dfrac{b}{\gcd(a, b)}k, y = y_0 - \dfrac{a}{\gcd(a, b)}k, k \in \mathbb{Z}$ 。下面是把 $x$ 框到非负数中。

int g = exgcd(a, b, x, y);
if (c % g) {
	// no solution
}
x *= a / g;
int t = b / g;
x = (x % t + t) % t;

ExCRT

souvenir

解同余方程组。因为 ExCRT 没比 CRT 难到哪里去且应用更广，直接上 ExCRT 就行。

模板：给定 $2n$ 个正整数 $a_1,a_2,\cdots ,a_n$ 和 $m_1,m_2,\cdots ,m_n$ ，求一个最小的正整数 $x$ ，满足 $\forall i\in[1,n],x\equiv a_i\ (\bmod m_i\ )$ ，或者给出无解。

faire

重点思想：合并。

考虑合并两条方程 $x \equiv a_1 \ ( \bmod m_1\ ), x \equiv a_2 \ ( \bmod m_2\ )$ 。则 $x = m_1k_1 + a_1 = m_2k_2 + a_2$ ， $m_1k_1 - m_2k_2 = a_2 - a_1$ 。Exgcd 可求出 $k_1, k_2$ ，又知道 $x$ 的差为 $\operatorname{lcm}(m_1, m_2)$ ，这就是合并后的 $m'$ 。
然后随便代一个 $x = m_1k_1 + a_1 = m_2k_2 + a_2$ 能算 $a'$ 。逐条合并即可。

int excrt() {
	for (int i = 2; i <= n; i++) {
		int g = exgcd(m[1], m[i], x, y);
		int c = a[i] - a[1];
		if (c % g) return -1;
		x *= c / g;
		int t = m[i] / g;
		x = (x % t + t) % t;
		int l = m[1] / __gcd(m[1], m[i]) * m[i];
		a[1] = (m[1] * x + a[1]) % l;
		m[1] = l;
	}
	return a[1];
}

quelque chose

注意可能需要开 __int128？

2-SAT

souvenir

一般就是每个变量为 $0 / 1$ （互斥），给出很多个关于两个变量的约束然后求解啥的。下文设 $x$ 表示 $1$ ， $x'$ 表示 $0$ 。比如 $x \oplus y = 1$ ，则连边 $x \to y'$ ， $x' \to y$ ， $y \to x'$ ， $y' \to x$ （单向的）。 $x \to y'$ 意思是”如果选了 $x$ ，为了使 $x \oplus y = 1$ ，只能有 $y'$ 。

faire

可以暴力 DFS。时间复杂度 $\mathcal O(n ^ 2)$ 。

bool dfs(int u) { // 这份代码 u ^ 1 为反集
	if (vis[u]) return true;
	if (vis[u ^ 1]) return false;
	vis[u] = true;
	s.push(u);
	for (const int &v : e[u])
		if (!dfs(v))
			return false;
	return true;
}


for (int i = 0; i < 2 * n; i += 2)
	if (!vis[i] && !vis[i + 1]) {
		while (s.size()) s.pop();
		if (!dfs(i)) {
			while (s.size()) vis[s.top()] = false, s.pop();
			if (!dfs(i + 1)) return cout << "NIE" << endl, 0;
		}
	}
for (int i = 0; i < 2 * n; i += 2)
	if (vis[i + 1]) cout << i + 2 << endl;
	else cout << i + 1 << endl; // 这个是当时编号，输出加了 1

也可以用 Tarjan 强连通分量缩点，根据所在强连通分量编号确定。时间复杂度 $\mathcal O(n + m)$ 。

void dfs(int u, int fa) {
	dfn[u] = low[u] = ++cnt;
	s.push(u);
	for (const int &v : e[u]) {
		// if (v == fa) continue;
		if (!dfn[v]) {
			dfs(v, u);
			low[u] = min(low[u], low[v]);
		}
		else if (!scc_id[v]) low[u] = min(low[u], dfn[v]);
	}
	if (low[u] == dfn[u]) {
		int t;
		scc_cnt++;
		do {
			t = s.top(); s.pop();
			scc_id[t] = scc_cnt;
		} while (t != u);
	}
}

for (int i = 1; i <= 2 * n; i++)
	if (!dfn[i]) dfs(i, i);
for (int i = 1; i <= n; i++)
	if (scc_id[i] == scc_id[i + n])
		return cout << "IMPOSSIBLE" << endl, 0; // 在同一强连通分量中（可互相到达）则无解
cout << "POSSIBLE" << endl;
for (int i = 1; i <= n; i++)
	cout << (scc_id[i] > scc_id[i + n]) << " ";

quelque chose

如果要确定字典序最小啥的，只能上 DFS。

关于 DFS 解的构造，看代码 $vis$ 数组显然；关于 Tarjan 解的构造，如果 $x$ 和 $x'$ 在同一 SCC 中无解，否则设 $scc\_id_i$ 表示 $i$ 的 SCC 编号，选更小的就好。也就是说，如果 $scc\_id_x < scc\_id_{x'}$ 就选 $x$ ，否则选 $x'$ 。证明见解的构造。

如果强制 $x$ 为 $0$ ，可以连边 $x \to x'$ ，vice versa。感性理解就是”即使你选了 $1$ ，也给我来到 $0$ “。

一道题目中，不同的 $x$ 和 $x'$ 含义可能不同，但是只要每个 $x$ 只有 $x$ 和 $x'$ 就能 2-SAT。如游戏。

Kruskal 重构树

souvenir

很神奇的树。

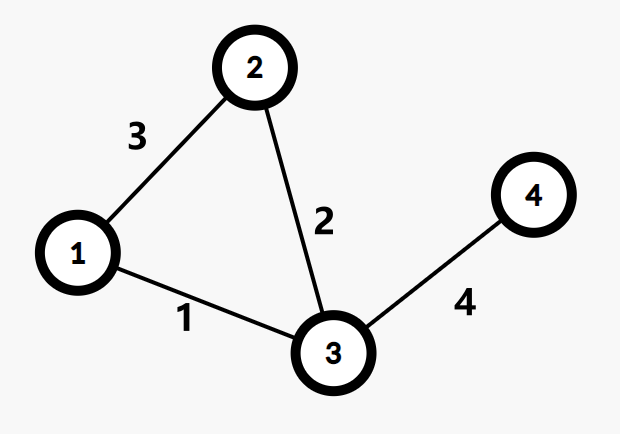
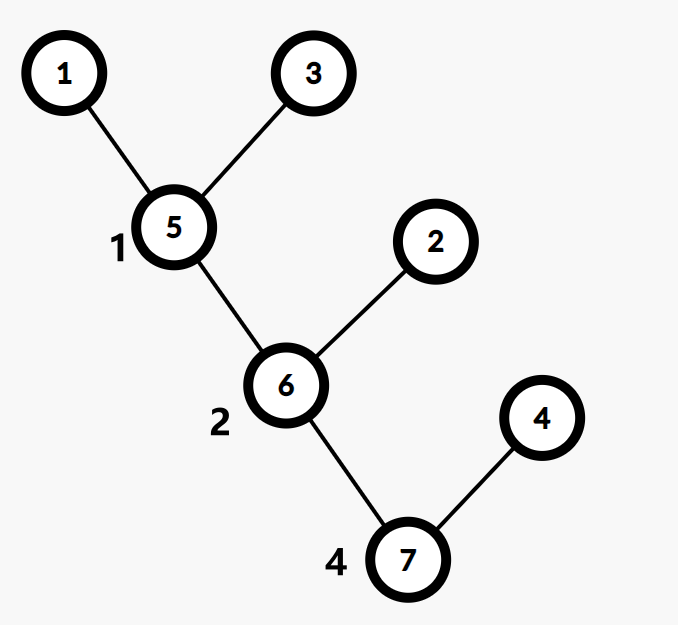
faire

在 Kruskal 跑生成树，合并两点的时候，新建一个点，并在点上维护信息（如两点之间边权），并以这两点作为儿子，就能建出 Kruskal 重构树。细节看代码。

时间复杂度就是 Kruskal 的。

void kruskal() {
	for (int i = 1; i <= 2 * n - 1; i++) fa[i] = i, a[i] = 0, e2[i].clear();
	sort(edge + 1, edge + 1 + m, [](node a, node b){ return a.a < b.a; });
	tot = n;
	for (int i = 1; i <= m; i++) {
		int x = find(edge[i].u), y = find(edge[i].v);
		if (x == y) continue;
		a[++tot] = edge[i].a;
		merge(x, tot);
		merge(y, tot);
		e2[tot].push_back(x);
		e2[tot].push_back(y);
	}
}

quelque chose

下面都是按照上图，边权从小到大建 Kruskal 重构树。

可以认为 Kruskal 重构树保存了每个历史版本的并查集连接信息，有点像可持久化并查集。

两点第一次连通时连通的边的边权，等于重构树上 LCA 的权值。

原图中两个点之间的所有简单路径上最大边权的最小值，等于最小生成树上两个点之间的简单路径上的最大值，等于 Kruskal 重构树上两点之间的 LCA 的权值。

由于树上建的点依次走下去，有单调性，可以倍增跳到最高的满足一些条件的点（如权值 $\leq p$ ），这个点的子树都满足 $\leq p$ ，就转化为了区间操作。可以 DFS 序与神秘数据结构结合，如维护第 $k$ 大： Peaks。可能的倍增写法：

for (int i = 18; ~i; i--)
	if (f[v][i] && a[f[v][i]] <= x) v = f[v][i];

Tarjan 相关

souvenir

主要就是割点、割边（桥）、点双连通分量、边双连通分量、强连通分量。下面一堆 definition 来袭。

割点，就是删掉这个点后图不连通。

割边，就是删掉这条边后图不连通。

在一张连通的无向图中，对于两个点 $u$ 和 $v$ ，如果无论删去哪个点（只能删去一个，且不能删 $u$ 和 $v$ ）， $u, v$ 都连通，则 $u, v$ 点双连通。

在一张连通的无向图中，对于两个点 $u$ 和 $v$ ，如果无论删去哪条边（只能删去一条）， $u,v$ 都连通，则 $u, v$ 边双连通。

强连通分量中，对于任意两个点 $u, v$ ， $u, v$ 都连通。

所以，，才发现不同的 $low_u$ 定义是不一样的吗。。。~~wssb。~~

faire

割点如果不是根节点，设 $v$ 是 $u$ 的儿子，若 $low_v \geq dfn_u$ ，即 $v$ 不能走到 $u$ 点“前面”的点，则 $u$ 为割点；如果是根节点，看有多少子树， $> 1$ 则为割点。

割边类似，如果 $dfn_v > low_u$ ，即 $v$ 不能走到 $u$ 点本身，则 $(u, v)$ 就是一条割边。

单调队列

Exgcd

souvenir

faire

quelque chose

ExCRT

souvenir

faire

quelque chose

2-SAT

souvenir

faire

quelque chose

Kruskal 重构树

souvenir

faire

quelque chose

Tarjan 相关

souvenir

faire

Modern English 转换 Early Modern English 速成指南（莎士比亚风）

Adventure of Ruby