liuzimingc's inner world

因为众所周知的原因，这套教材 A 类和 B 类写得尤其烂，像是微积分，空间向量与代数啥的。所以主要看看 C 和 D。下面是一些简单的感想和总结。

逻辑推理初步 C 类

区分了一个否命题和否定命题。$p \to q$ 的否命题是 $\lnot p \to \lnot q$，否定命题是 $p \to \lnot q$，逆否命题是 $\lnot q \to \lnot p$。原命题等价于逆否命题，这就是反证法的内在逻辑。

讲同一律的时候引入了恩格斯的批判来说「如果在历史发展的长河中认识问题，同一律就显得僵化了」。有点神奇。

讲了一个庞加莱猜想，引入的概念非常难以理解。

讲完全归纳法时提到了四色猜想（当然已经被证明了），是真的分成了 1936 种情况然后用计算机验证的。很厉害啊。

好神秘的证明方法。搜索了一下，好像确实是类似这么证的。

公设就是「无法推出的前置」，公理就是可以推出的。

具体讲述了欧式几何和非欧几何的区别：第五公设，即平行公设。

欧式几何的公设：

1. 从一点向另一点可以引一条直线。
2. 任意线段能无限延伸成一条直线。
3. 给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
4. 所有直角都相等。
5. 过一点只能作一条与已知直线不相交的直线。

简单介绍的话，双曲几何就是类似于薯片，上面的直线会略微偏向薯片中心，像这样：

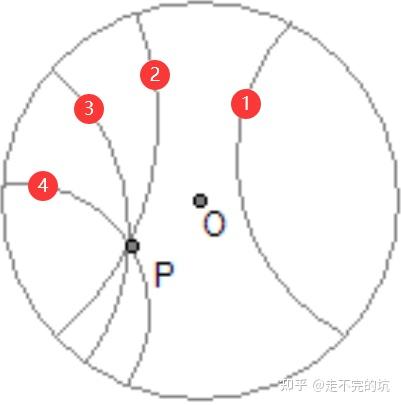
过 P 点有多条直线与已知直线不相交。进一步可以看：Link。

而黎曼几何就是一个地球，直线为「大圆」，可以想成赤道 / 经线，那么任意两条大圆总会相交。这部分还挺好玩的。

然后讲了一个阿罗不可能定理：与 ChatGPT 的交流。尝试具体证明，但是发现会涉及很难的东西，遂放弃。

又有一个哥德尔不完备性定理：

第一个不完备性定理指出，没有一个一致的公理系统，其定理可以通过有效的程序（即算法）列出，能够证明关于自然数算术的所有真理。对于任何此类一致的正式系统，总会有关于自然数的陈述是真实的，但在系统内是无法证明的。

第二个不完备性定理是第一个不完备性定理的扩展，表明系统无法证明其自身的一致性。

还是看不懂。润了。

总结：纯知识部分是陈波《逻辑学十五讲》的真子集，和政治选必三《逻辑和思维》差不多。补充的一些东西比较有趣，可以看看。