liuzimingc's inner world

其实就是简记一下单调栈的一个很好的理解方式，来源 writings.sh。

以单调递减的单调栈为例。因为如果要加入元素肯定都要先依次弹出栈顶，使加入新元素后能满足单调性。这里就是弹出不比新元素大的栈顶。假设目前准备加入一个新元素 $x$，正在弹栈（栈顶是需要被弹出的，$s_{top}$），栈底是 $s_0$。那么，有如下的性质：

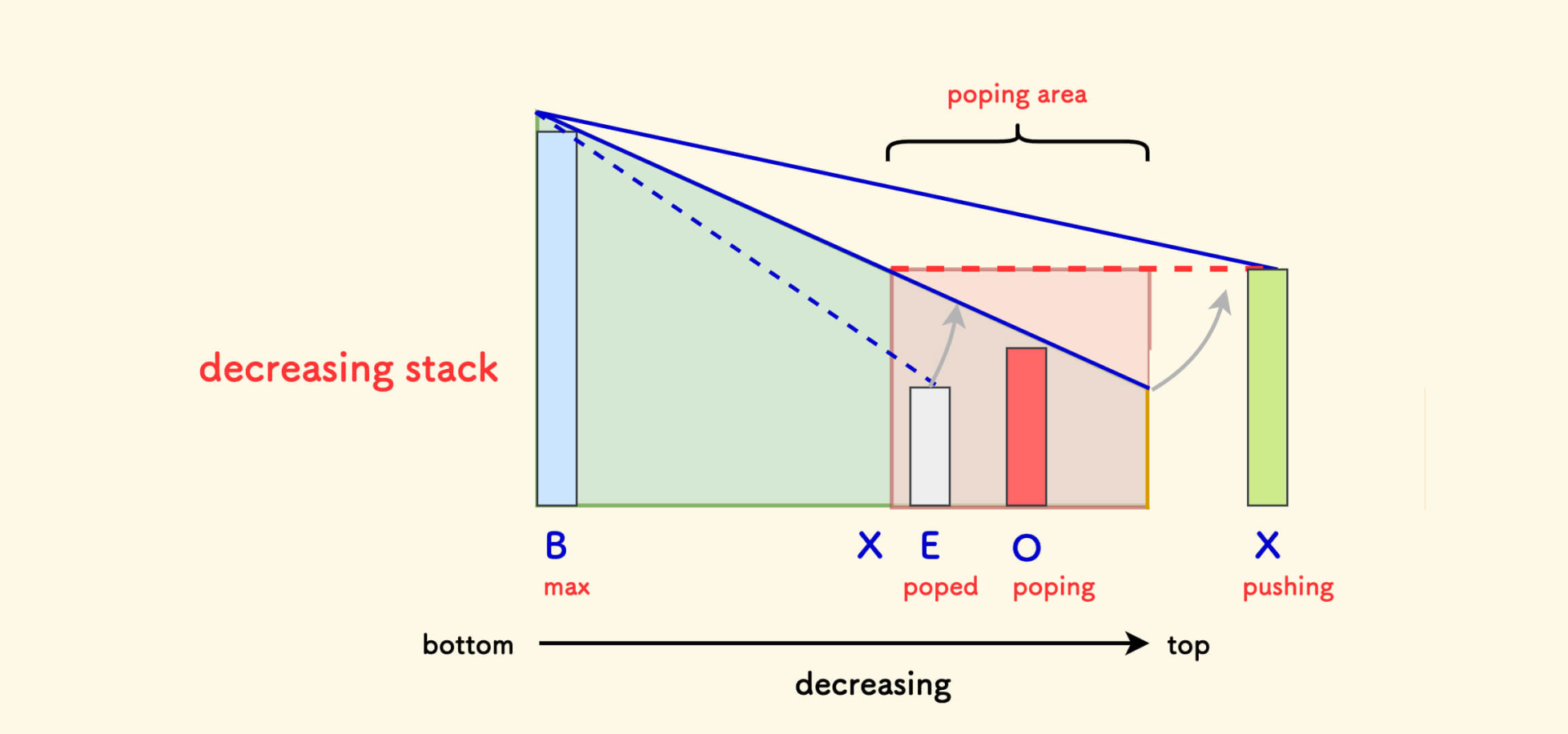
1. $s_{top} \leq x$。按弹出的定义就有了。
2. $s_0$ 一定是目前扫到的最大值。否则一定会有元素使它被弹出。
3. $s_{top}$ 在原数组中下一个不比它小的元素为 $x$。因为如果中间存在一个不比它小的元素，一定会在 $x$ 之前使它被弹出。这个可以解决 NGE（Next Greater Element）问题。
4. 假设 $x$ 已经弹出了一些栈中元素，那么由 1 有 $s_{top} \leq x$，又因为栈是单减的，有 $lst < s_{top}$。这就是 “$x$ 的局部长板效应”：$lst < s_{top} \leq x$。
5. $s_{top}$ 是在栈内上一个元素 $s_{top - 1}$ 和 $x$ 之间（不含端点）的最大元素。首先由 3 可以得到一部分，而如果在 $s_{top - 1}$ 到 $s_{top}$ 之间存在比 $s_{top}$ 更大的元素 $nul$，假设 $nul$ $\geq s_{top - 1}$，$s_{top - 1}$ 就会被弹出，矛盾；而如果 $s_{top - 1} > nul > s_{top}$，它就会存在于栈中 $s_{top - 1}$ 和 $s_{top}$ 之间，但是栈中 $s_{top - 1}$ 和 $s_{top}$ 之间显然没有元素，矛盾。这就是 “$s_{top}$ 的局部长板效应”。和悬线法有点关系，也可能用于更新贡献（$s_{top - 1} + 1$ 到 $s_{top}$ 的位置，见 Pudding Monsters）。

顺便说一下悬线法。感觉更适用于单个元素扩展的感觉（有点像笛卡尔树）。

诶多，悬线法还是挺帅气的 (′д｀ )…彡…彡，至少随便处理个啥的都很优雅：

for (int i = 1; i <= n; i++) l[i] = r[i] = i;
for (int i = 1; i <= n; i++)
	while (l[i] > 1 && a[i] < a[l[i] - 1]) l[i] = l[l[i] - 1];
for (int i = n; i; i--)
	while (r[i] < n && a[i] <= a[r[i] + 1]) r[i] = r[r[i] + 1];